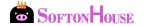有名なアインシュタインの質量とエネルギーの等価式です。
この方程式は単純に見えますが、感覚的に説明するのが難しいですよね。
核が分裂すると陽子と中性子になりますが、何故か実際の原子核の方が、陽子と中性子の総和より小さいのです。
その事を「質量欠損」と呼んでいて、その差は原子核内部の結合エネルギーであるというものです。核の中にエネルギーが隠れているのですね。
で、そのエネルギーをどう表すかと言うと、E=mc^2と表すのです。
光の速度はどこから見ても一定であり、電磁波のような波動も光速で移動できるという根本的な理屈があるので、ローレンツ変換などの式によりこのような式が証明できるという事です。
また、この式は E=1/2・mv^2 という運動エネルギーの式ではなく、核分裂によって生じる「質量欠損」部分のエネルギーを表す公式であり、運動していなくとも「そもそも持っているエネルギー」という事です。
質量保存の法則から、化学反応を起こしても質量は変わりませんが、核分裂は「質量欠損」の分変わってしまい、その部分がエネルギーとして放出されるのです。そう、原爆の仕組みです。
物体は運動していなくともエネルギーを持っているから、原爆みたいなものが作れるという訳ですね。
数式だと当然そうなる事でも、数式を利用せず説明しようとすると、かなり難しいのがこの公式です・・・。
ところで、E=mc^2 の式では、光の粒子のような質量ゼロのものについて説明ができません。つまり、この式は完全ではありません。
今まで私がこの公式を考えるうえで、数学の知識があればなんとなく理解できる HP がありますので、それを参照してみてください。
http://homepage2.nifty.com/eman/relativity/4momentum.html
なぜ c^2 なのかというと、それは光を基準にして式を作らないと、その式が成り立たないからです。
光より早い粒子が発見されると、この公式も変わるかもしれません。
未来に期待です。